leetcode36 有效的数独【中等难度】|极客学长
# 36. 有效的数独 (opens new window)
# 英文题目: Valid sudoku
| ● 难度: | 中等 |
请你判断一个 9x9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。（请参考示例图）
数独部分空格内已填入了数字，空白格用 '.' 表示。
注意：
- 一个有效的数独（部分已被填充）不一定是可解的。
- 只需要根据以上规则，验证已经填入的数字是否有效即可。
示例 1：
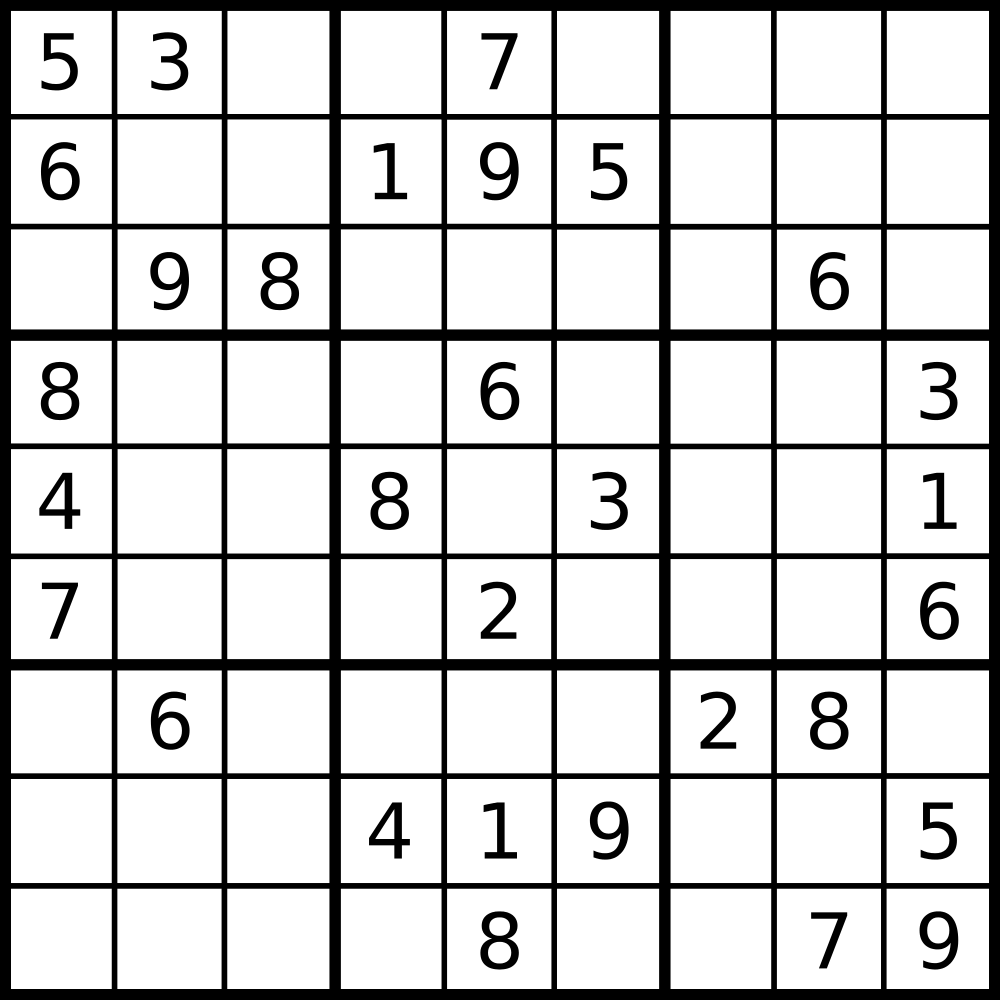
输入：board =
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：true
1
2
3
4
5
6
7
8
9
10
11
2
3
4
5
6
7
8
9
10
11
示例 2：
输入：board =
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：false
解释：除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。
1
2
3
4
5
6
7
8
9
10
11
12
2
3
4
5
6
7
8
9
10
11
12
提示：
board.length == 9board[i].length == 9board[i][j]是一位数字或者'.'
# 分析
# 方法1、蛮力直接法
使用set， 对于行遍历: 每一行中, isValid: unique的数字数量+'.'的数量 = 9, 对于列遍历：每一列中, isValid: unique的数字数量+'.'的数量 = 9, 对于box遍历：每个3行3列九宫格中，isValid: unique的数字数量+'.'的数量 = 9。
已AC代码:
class Solution {
public:
bool isValidSudoku(vector<vector<char>> &board)
{
bool isValid = true;
// 遍历行
for (int i = 0; i < 9; i++)
{
set<char> st;
vector<char> rowVec = board[i];
int dotCount = 0;
for (int k = 0; k < 9; k++)
{
if (rowVec[k] == '.')
{
dotCount++;
}
else
st.insert(rowVec[k]);
}
int uniqueCharCount = st.size();
if (uniqueCharCount + dotCount != 9)
{
isValid = false;
}
}
// 遍历列
for (int i = 0; i < 9; i++)
{
set<char> st;
int dotCount = 0;
for (int k = 0; k < 9; k++)
{
if (board[k][i] == '.')
{
dotCount++;
}
else
st.insert(board[k][i]);
}
int uniqueCharCount = st.size();
if (uniqueCharCount + dotCount != 9)
{
isValid = false;
}
}
// 遍历小grid: 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
for (int si = 0; si <= 6; si += 3)
for (int sj = 0; sj <= 6; sj += 3)
{
set<char> st;
int dotCount = 0;
for (int i = si; i < si + 3; i++)
{
for (int j = sj; j < sj + 3; j++)
{
if (board[i][j] == '.')
dotCount += 1;
else
st.insert(board[i][j]);
}
}
if (st.size() + dotCount != 9)
isValid = false;
}
return isValid;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
跟国外的小伙伴想到一块去了。 https://leetcode.com/problems/valid-sudoku/discuss/869625/easy-C%2B%2B-with-set (opens new window)
# 方法2：set插入方法 - 改进
坐标中任意一点(i,j)，可以map到对应的的第几行第几列的方块(box)中，box的坐标为(i/3, j/3)。
于是把一个小的九宫格中的数全压缩到一个box中，比如：
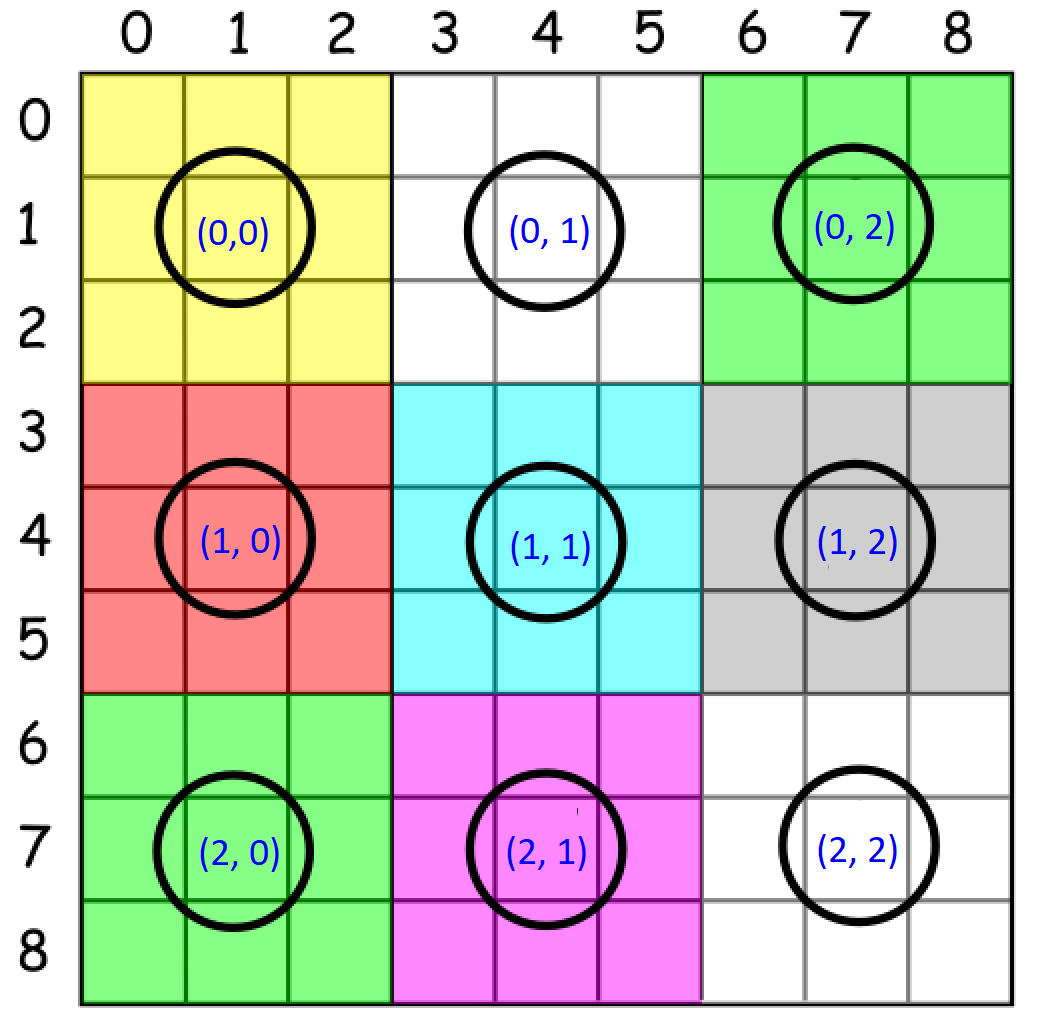
以最中间那个九宫格为例，使用int型的/3可以得到:
对于任意一个值不为'.'的字符，进行如下操作:
1.把所在row的信息插入到大九宫格中;
2.把所在column的信息插入到大九宫格中;
3.把所在的小方块(box)的信息插入到大九宫格中。
插入如果失败说明出现了重复。
# 已AC的C++代码:
class Solution {
public:
bool isValidSudoku(vector<vector<char>>& board) {
set<string> st;
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
char ch = board[i][j];
// 使用i / 3 + "," + j / 3 得到对应第几行第几列的方块(box)
if (ch != '.'){
string val;
val.push_back(ch);
/* 对于任意一个值不为'.'的字符
1.把所在row的信息插入到大九宫格中;
2.把所在column的信息插入到大九宫格中;
3.把所在的小方块(box)的信息插入到大九宫格中。
插入如果失败说明出现了重复。 */
if (!st.insert(val + " in row " + to_string(i)).second ||
!st.insert(val + " in column " + to_string(j)).second ||
!st.insert(val + " in box " + to_string(i / 3) + "," + to_string(j / 3)).second)
return false; /* set插入失败时，表示出现了重复 */
}
}
}
return true;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Java的HashSet有同样的写法，Java中插入失败，会出现 set.Add() == false。
# 方法3：使用位操作
此题，使用位操作，是几种解法中速度最快的算法了。
具体做法是：
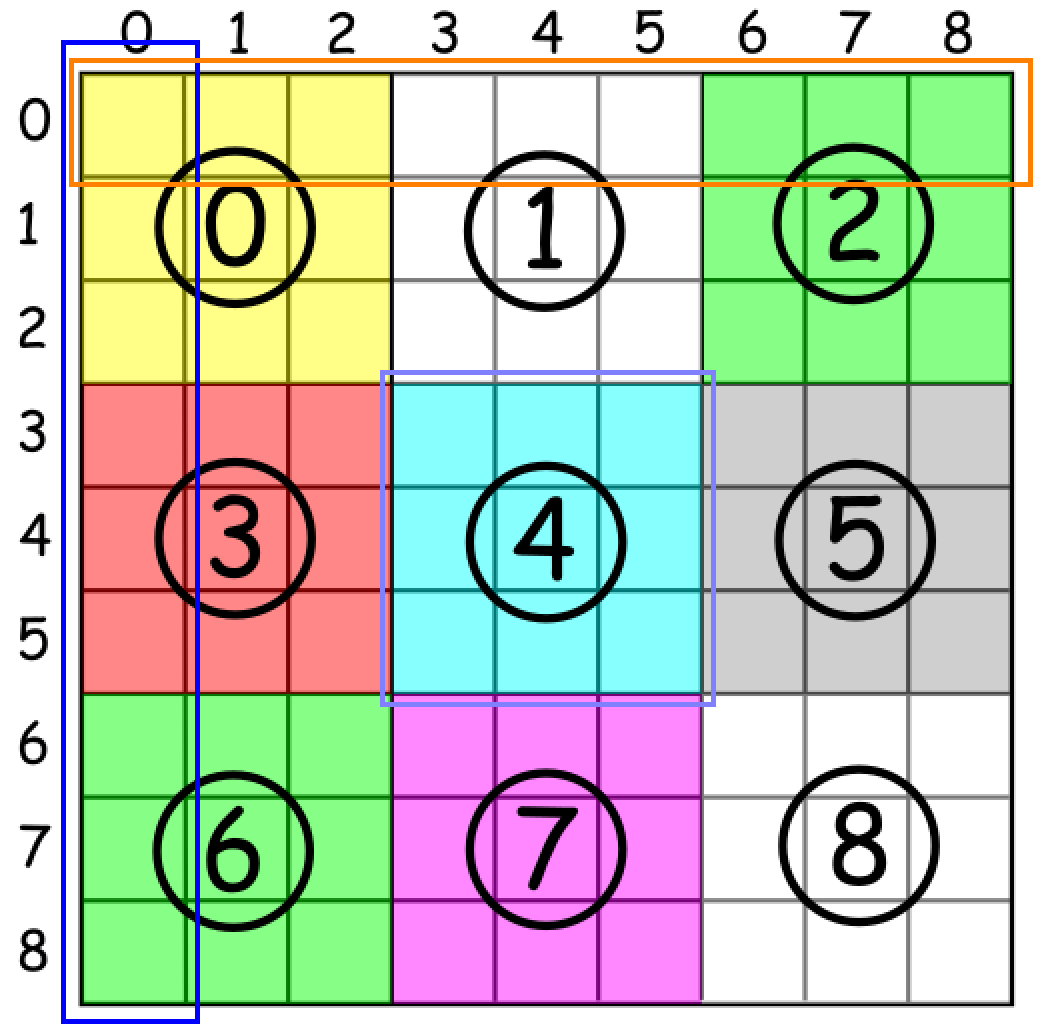
将大数独棋盘分成9个小棋盘，编号0~8。
窗口中的每个小方格若有数字，必为 1 ~ 9 (记作k)，该方法适用于 遍历行/遍历列/遍历box。
然后把 二进制数 1 左移 k 位，得到偏移量shift，后续使用按位或|来判断是否存在。
# 已AC的C++代码:
class Solution {
public:
bool isValidSudoku(vector<vector<char>>& board) {
vector<int> row(9); // row[j]表示第j 行的9个数字各自的存在情况，同理于col, boxes
vector<int> col(9);
vector<int> boxes(9);
int shiftInt = 0;
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 9; j++)
{
if (board[i][j] == '.')
continue;
shiftInt = 1 << (board[i][j] - '0'); // 转为二进制，移位结束后目标位为1，其他位均为0
/* 每个格子若有数字，必为 1 ~ 9，该方法适用于 遍历行/遍历列/遍历box */
int boxPos = (i / 3) * 3 + j / 3; //将大数独棋盘分成9个小棋盘，编号0~8
// 如果当前数字shiftInt在row[j] 或col[i] 或 boxes中已经存在，&运算后不为0，
// 只有当前数字没出现过，&运算后为0
if ((col[i] & shiftInt) != 0 || (row[j] & shiftInt) != 0 || (boxes[boxPos] & shiftInt) != 0)
return false;
//第 n 位代表 n 这个数字是否存在(1→存在， 0→不存在)，同理于col[i] boxes[boxPos]
row[j] |= shiftInt;
col[i] |= shiftInt;
boxes[boxPos] |= shiftInt;
}
}
return true;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
后两种方法，参考:
https://www.youtube.com/watch?v=ceOLAY4XUOw&ab_channel=JacobHuang (opens new window)
编辑 (opens new window)
上次更新: 2021/10/30, 12:58:38